1.Basic Characteristics of Aluminum in Capacitor Aluminum Foil
Aluminum is the 13th element in the periodic table, with a relative atomic mass of 26.98, a melting point between 660 and 661°C, and a room temperature density of 2.699g/cm3, which is a light metal. Aluminum has very good electrical conductivity. Pure aluminum with a purity greater than 99.995% has a resistivity of 2.62×10-8~2.65×10-8Ω·m at 60°C. Aluminum has high thermal conductivity, which is about 55% of copper. Aluminum has the lowest thermal conductivity at room temperature, but it is still as high as 235~237W/(m·K). Aluminum is a paramagnetic material and will not be magnetized, so it will not be affected by the magnetic field.,The above is an explanation of the basic properties of capacitor aluminum foil-aluminum.
Aluminum has excellent plasticity. High-purity aluminum with a content of 99.999% Al has a room temperature elongation of more than 70%. Aluminum has low deformation resistance and can be easily processed by forging, rolling, extrusion, etc., and made into plates, foils, and wires. The good plasticity of aluminum also makes large deformation and high-speed deformation processing possible, so aluminum has good deformation and forming processing performance. Due to the low deformation resistance of aluminum, aluminum can also be processed by high-speed turning, milling, boring, planing, grinding, etc. Below 0°C, as the temperature decreases, the plasticity of aluminum will not only not decrease, but will increase. There is no low-temperature brittleness, and it can be used in many low-temperature occasions. The strength of pure aluminum is relatively low. The room temperature yield strength of high-purity aluminum with a content of 99.999% Al is only 15~20MPa, and the tensile strength is only 40~50 MPa. High-purity aluminum has no phase change, and the strength of aluminum can be improved by work hardening. When cold rolled 90%, the yield strength of pure aluminum can reach 100~120MPa, and the tensile strength can reach 120~140MPa
A dense and firm Al2O3 protective film is easily formed on the surface of aluminum. This protective film will only be destroyed under the intense action of halogen ions or alkali ions. The casting performance of pure aluminum is usually poor. The temperature range from the beginning to the end of solidification of pure aluminum is very narrow. Due to its good thermal conductivity, large temperature fluctuations are likely to occur in various parts of the solidified body during solidification. When the purity is 99.996% AI, the liquid density at the solidification point is 2.37 g/cm 3, while the solid density is 2.55 g/cm 3. The solidification shrinkage is 7%, so shrinkage cavities are easy to appear in pure aluminum ingots. The high thermal expansion coefficient and crystallization shrinkage rate of aluminum are also easy to cause thermal stress. Liquid aluminum can dissolve a large amount of hydrogen, but solid aluminum hardly dissolves hydrogen. When solidification is fast and cooling, hydrogen is not easy to precipitate, so it is easy to cause pores in the aluminum ingot. Even very high-purity aluminum inevitably contains a small amount of impurity elements, among which the most common trace elements are Cu, Si, Fe, Mg, etc.
2.Capacitor Aluminum Foil-Crystal Structure
Pure aluminum widely used in industry is composed of a large number of aluminum atoms gathered and stacked. Studies have shown that these atoms are not randomly stacked, but are arranged very regularly. Figure 1.1 shows the microscopic regular arrangement of aluminum atoms observed from two different directions using a high-resolution electron microscope. Regardless of the direction from which it is observed, the three-dimensional arrangement of aluminum atoms is regular and orderly, which is called three-dimensional long-range ordered arrangement. Objects composed of three-dimensional long-range ordered arrangement of atoms can be called crystals, so aluminum is a crystal.

Theoretical research and experimental detection show that the stacking and regular arrangement of aluminum atoms in three-dimensional space are shown in Figure 1.2(a); for the sake of clarity, Figure 1.2(a) only draws the arrangement of the outer atoms when aluminum atoms are stacked in three-dimensional space, and does not draw the aluminum atoms behind the outer atoms. Among a large number of regularly arranged atoms, if a limited group of atoms are selected within a specific unit body range and arranged irregularly and repeatedly in three-dimensional space, the three-dimensional structure of the aluminum crystal shown in Figure 1.2(a) can be constructed. Although there are many ways to select the unit body range, in actual selection, the unit body range is often required to be as small as possible, and the shape parameters of the unit body should reflect the rotational symmetry characteristics of the crystal as much as possible. If the space occupied by a group of dark gray atoms in Figure 1.2(a) is selected as the unit body range, the three-dimensional arrangement of atoms in the unit body is shown in Figure 1.2(b), and the unit body is called the unit cell of the aluminum crystal; from the perspective of observation, the aluminum atoms behind the outer atoms are represented by light gray dotted lines.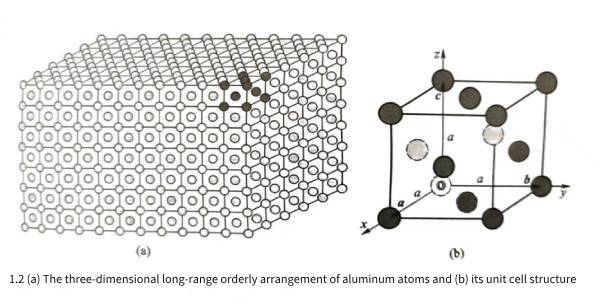
As shown in Figure 1.2(b), let the atom marked as “o” in the unit cell be the origin, and let the three edges of the unit cell be the three crystal axes x, y, and z. The vectors of the three edges are the unit cell vectors a, b, and c. It can be imagined that the unit cell of Figure 1.2(b) is periodically translated up, down, left, right, forward, and backward along the three axes x, y, and z, and the translation vectors are any integer multiples of “a, b, and c”. All the unit cells before and after the translation are accumulated together to construct an aluminum crystal three-dimensional structure of any size and shape as shown in Figure 1.2(a).
Experimental analysis and detection show that the aluminum unit cell vectors a, b, and c are perpendicular to each other, and the lengths of the three vectors are equal; therefore, it can be seen that the unit cell shown in Figure 1.2(b) is actually a cube. Let a be the length of the unit cell edge, called the unit cell constant; X-ray detection shows that a is 0.40491nm. Observing the atomic distribution in the aluminum cube unit cell, it can be found that the cube is constructed by 6 square surfaces: top, bottom, left, right, front, and back. There is an aluminum atom in the center of each square surface; this atomic arrangement structure is a face-centered cubic structure, so aluminum belongs to the face-centered cubic crystal in the cubic crystal system. The distance between the centers of each atom in the aluminum unit cell is not the same. The nearest neighbor atom is the neighboring atom in the diagonal direction of each square surface. The distance between the centers of the atoms is half of the diagonal. The distance between the nearest neighbor atoms in the aluminum crystal is represented by b. According to the unit cell constant a, b=0.2863nm can be calculated, which is the distance between the nearest neighbor atoms observed in Figure 1.1. The distance between adjacent atoms in aluminum crystals is very small relative to the macroscopic size of the crystal. Therefore, when analyzing and discussing the microstructure of aluminum crystals, it is often regarded as an infinitely large object, that is, it is approximately considered that the aluminum crystal is composed of its unit cell three-dimensional infinite periodic arrangement.
The above is an explanation of Capacitor aluminum foil-crystal structure.
3 Capacitor Aluminum Foil – Crystal Direction And Crystal Plane
It can be observed from Figure 1.1 and Figure 1.2(a) that there are significant differences in the density of atomic arrangement in different directions in the three-dimensional periodic aluminum crystal. In order to facilitate the analysis and discussion of the characteristics of aluminum atoms arranged in different directions, it is necessary to use crystal direction indices to describe different crystal directions (referred to as crystal directions). Imagine that the origin atom in Figure 1.2(b) is connected to any atom in the crystal with x, y, and z coordinate values of pa, ma, and na respectively. The vector r formed can form a crystal direction, where a is the unit cell constant and: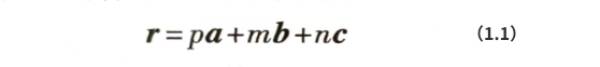
Simplify p, m, and n into three mutually prime integers u, v, and w in proportion, and then use [uvw] to express the crystal direction index of vector r. If there is a negative number in u, v, and w, take the absolute value of the negative number and add a horizontal line above the number; for example, the crystal direction index of u:v:w=-1/2:1/2:1=-1∶1:2 is [112]
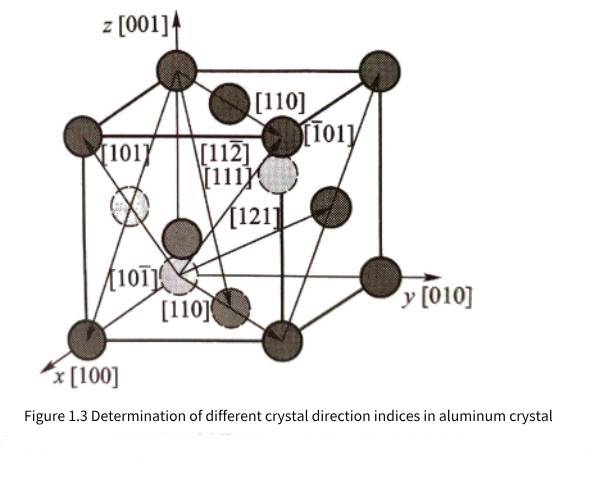
When analyzing the crystal direction, any atom in the crystal can be regarded as the origin atom. Figure 1.3 gives some examples of crystal direction indices in the aluminum crystal coordinate system. Crystal directions that are parallel to each other and in the same direction have the same crystal direction index; crystal direction indices [uvw] and [uvw] are parallel to each other but in opposite directions. It can be seen that the x, y, and z crystal axes of the aluminum crystal constitute the crystal coordinate system for observing the atomic distribution in the aluminum crystal; if expressed in terms of crystal directions, the [100], [010], and [001] crystal directions of the aluminum crystal constitute the three basic crystal axes of the crystal coordinate system.
 It can also be observed in Figure 1.1 and Figure 1.2(a) that the density and rules of atomic arrangement on different planes of three-dimensional periodic aluminum crystals are different. In order to facilitate the analysis and discussion of the characteristics of aluminum atoms arranged on different planes, it is necessary to use crystal plane indices to express crystal planes (referred to as crystal planes). Imagine the distance from the intersection of any plane with the three crystal axes in Figure 1.2(b) to the origin, that is, the three intercepts are pa, ma, and na, and then 1/p=h, 1/m=k, and 1/n=l, so a/h=pa, a/k=ma, and a/l=na are also the lengths of the intercepts of the plane on the three coordinate axes. Usually, h, k, and l are simplified to mutually prime integers and (hkl) is used as the crystal plane index. When p, m, and n are not integers (hkl), the intersection with the three crystal axes may not be the atomic position. When the crystal plane is parallel to a certain coordinate axis, the reciprocal of the corresponding intercept is zero, that is, 0 will appear in the crystal plane index, such as (hk0), (h00), etc. In addition, (hkl) and (hkl) are exactly the same planes, but the normals of the selected crystal planes are opposite when observing (hkl) and (hkl) planes. Because the index values h, k, and l can be rounded and coprime, no matter where the crystal plane is located, the crystal plane index of mutually parallel crystal planes is the same. According to the needs of crystal detection technology, sometimes the values of h, k, and l will also have common factors, such as (200) (224), etc. Figure 1.4 shows examples of various crystal planes in aluminum crystals and their corresponding crystal plane indices.
It can also be observed in Figure 1.1 and Figure 1.2(a) that the density and rules of atomic arrangement on different planes of three-dimensional periodic aluminum crystals are different. In order to facilitate the analysis and discussion of the characteristics of aluminum atoms arranged on different planes, it is necessary to use crystal plane indices to express crystal planes (referred to as crystal planes). Imagine the distance from the intersection of any plane with the three crystal axes in Figure 1.2(b) to the origin, that is, the three intercepts are pa, ma, and na, and then 1/p=h, 1/m=k, and 1/n=l, so a/h=pa, a/k=ma, and a/l=na are also the lengths of the intercepts of the plane on the three coordinate axes. Usually, h, k, and l are simplified to mutually prime integers and (hkl) is used as the crystal plane index. When p, m, and n are not integers (hkl), the intersection with the three crystal axes may not be the atomic position. When the crystal plane is parallel to a certain coordinate axis, the reciprocal of the corresponding intercept is zero, that is, 0 will appear in the crystal plane index, such as (hk0), (h00), etc. In addition, (hkl) and (hkl) are exactly the same planes, but the normals of the selected crystal planes are opposite when observing (hkl) and (hkl) planes. Because the index values h, k, and l can be rounded and coprime, no matter where the crystal plane is located, the crystal plane index of mutually parallel crystal planes is the same. According to the needs of crystal detection technology, sometimes the values of h, k, and l will also have common factors, such as (200) (224), etc. Figure 1.4 shows examples of various crystal planes in aluminum crystals and their corresponding crystal plane indices.
Comparing and analyzing the structure of the aluminum crystal given in Figure 1.2 and the various possible crystal planes in the aluminum crystal shown in Figure 1.4, it can be found that Figure 1.1 (a) shows the atomic arrangement on the (100) plane of the aluminum crystal, and Figure 1.1 (b) shows the atomic arrangement on the (111) plane of the aluminum crystal.
According to the principle of determining the crystal plane and crystal direction index, it can be proved that for aluminum crystals, there is always a (hkl) crystal plane perpendicular to the [hkl] crystal direction, or [hkl] is the normal direction of (hkl).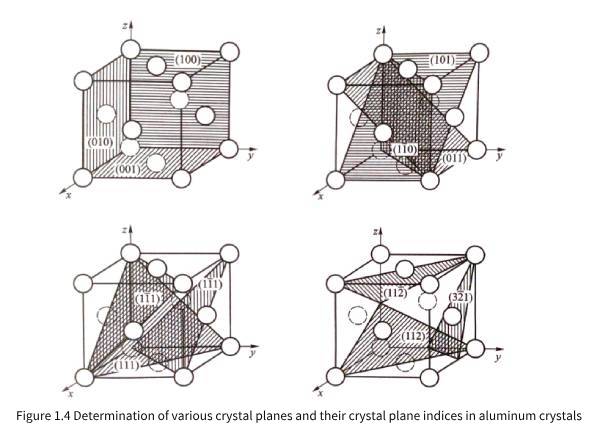
As shown in Figure 1.5, the spacing between different crystal planes and their parallel planes can be observed on the (001) plane of aluminum crystals. It is observed that changing the crystal plane index will affect the plane spacing between parallel crystal planes. It can be proved that the spacing d hkl between parallel (hkl) planes in aluminum crystals is related to the unit cell constant a by

The above is an explanation of capacitor aluminum foil-crystal directions and crystal planes.
4 Rotational Symmetry of Aluminum Crystals
Let the aluminum crystal rotate around the plane normal direction [001] passing through any atom on the (001) plane as shown in Figure 1.5; when the rotation angle is 90°, 180°, 270°, and 360°, the arrangement rules and relative positions of the atoms in the crystal before and after the rotation, including the (001) plane and all atoms above and below the plane, remain the same. This operation is called a symmetric rotation operation. Here, the rotation angle can be any integer multiple of 360°/4, and the symmetric rotation operation is called a 4-fold symmetric rotation operation, and the corresponding [001] direction is the 4-fold rotation axis. Generally, a symmetric rotation operation with a rotation angle of any integer multiple of 360°/n is called an n-fold symmetric rotation operation, and the corresponding rotation axis is the n-fold rotation axis, or the n-fold axis. Table 1.1 lists the rotational symmetry of various types of crystal directions in aluminum crystals, among which the [111] direction has a 3D symmetry, that is, after the crystal is rotated 120° around the [111] direction, the arrangement rules and relative positions of all atoms in the crystal are the same as before the rotation.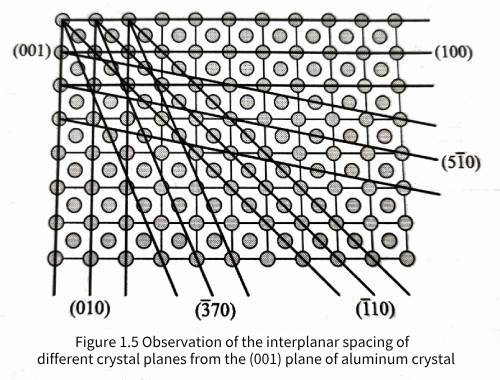
Table 1.1 Rotational symmetry n of different crystal directions in aluminum crystals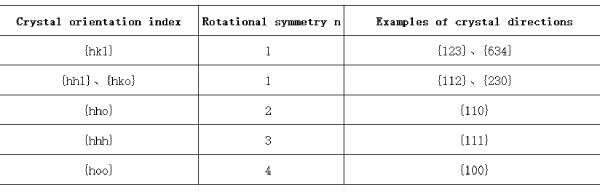 There are a large number of other non-parallel equivalent crystal planes in aluminum crystals. All equivalent crystal planes in a crystal are usually grouped into a group of crystal planes with common characteristics, called a crystal plane family, represented by hkl. Based on similar principles, some non-parallel crystal directions in aluminum crystals can have exactly the same atomic structure state and relative environment, and all atoms and their surrounding environments on them can also be completely overlapped one-to-one after corresponding rotational symmetry operations. All equivalent crystal directions in a crystal are usually grouped into a group of crystal directions with common characteristics, called a crystal direction family, represented by <uvw>. For example, [100], [010], [001] [100], [0 10] and [00 1] in aluminum crystals belong to the crystal direction family <100>, where [100], [010] and [001] are not parallel to each other; (111), (111), (1 11), (111), (111), (111) and (111) in aluminum crystals belong to the crystal plane family {111}, where (111), (111), (111) and (111) are not parallel to each other.
There are a large number of other non-parallel equivalent crystal planes in aluminum crystals. All equivalent crystal planes in a crystal are usually grouped into a group of crystal planes with common characteristics, called a crystal plane family, represented by hkl. Based on similar principles, some non-parallel crystal directions in aluminum crystals can have exactly the same atomic structure state and relative environment, and all atoms and their surrounding environments on them can also be completely overlapped one-to-one after corresponding rotational symmetry operations. All equivalent crystal directions in a crystal are usually grouped into a group of crystal directions with common characteristics, called a crystal direction family, represented by <uvw>. For example, [100], [010], [001] [100], [0 10] and [00 1] in aluminum crystals belong to the crystal direction family <100>, where [100], [010] and [001] are not parallel to each other; (111), (111), (1 11), (111), (111), (111) and (111) in aluminum crystals belong to the crystal plane family {111}, where (111), (111), (111) and (111) are not parallel to each other.
In any crystal direction [uvw] of aluminum crystal, different crystal directions formed by swapping the positions of the three characters u, v and w belong to the same crystal direction family, and the total arrangement is 6; when the three characters u, v and w are taken as positive or negative values and combined arbitrarily, all possible crystal directions also belong to the same crystal direction family, and the total number of possible combinations is 2x2x2=8. Therefore, there can be a total of up to 6×8=48 crystal directions with different index forms in the cubic crystal direction family <uvw>. When the three characters u, v or w in any crystal direction family <uvw> are taken as 0, the possibility of positive and negative value changes will be lost and the number of crystal directions will be reduced. When the characters and character values are equal among the three characters, the possibility of their position swapping will also decrease. Considering that [uww] and [uvw] are always parallel to each other in the above crystal directions, only half of all the crystal directions in the above crystal direction family are completely non-parallel. From this, the number of non-parallel crystal directions in the corresponding crystal direction family can be calculated. Similarly, the number of non-parallel crystal planes in the corresponding crystal plane family can also be calculated. Table 1.2 gives the number z of non-parallel crystal planes or crystal directions in all possible crystal plane families and crystal direction families in aluminum crystals.
Table 1.2 Number of non-parallel crystal planes or directions z in different crystal plane families and crystal direction families of aluminum crystals

The above is an explanation of the rotational symmetry of capacitor aluminum foil-aluminum crystals.
Summary:
Capacitor aluminum foil-This chapter mainly discusses the basic properties and crystal structure of aluminum, crystal orientation and crystal plane, and the rotational symmetry of aluminum crystals. For more information about capacitors please click:https://xuanxcapacitor.com




